Medidas de tendencia central

Los datos no agrupados son aquellos que, obtenidos a partir de un estudio, no están todavía organizados por clases. Cuando es un número manejable de datos, usualmente 20 o menos, y hay pocos datos diferentes, se pueden tratar como no agrupados y extraer información valiosa de ellos.

https://www.youtube.com/watch?v=fOuRqk1nzgY

Media aritmética

La media aritmética es la medida de tendencia central más utilizada y la de mayor representatividad en los análisis estadísticos. Representa el promedio del conjunto de datos de la muestra. Su cálculo se realiza con la suma de todos los valores de los datos, dividida entre el número de datos que componen la muestra.

Moda

En estadística, el concepto de la moda no se aleja de esta apreciación y, efectivamente, se denomina moda de un conjunto de datos al valor que más se presenta, es decir, el atributo o el valor de mayor frecuencia. La moda se representa por Mo y puede ser aplicada a las variables cualitativas y cuantitativas discretas o continuas.

Para obtener la moda de un conjunto de datos que están sin agrupar, se construyen las frecuencias y se ubica el valor o la característica que corresponde a la frecuencia mayor.

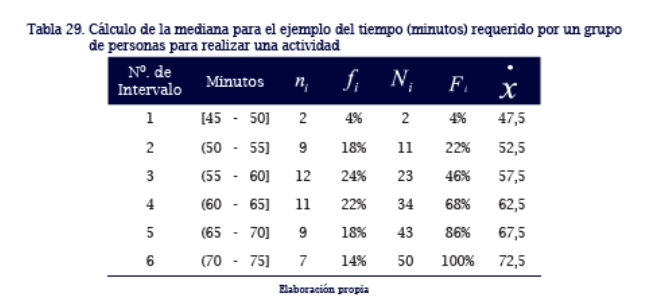
Mediana

La mediana en un conjunto de datos es el valor que ocupa el lugar central, de tal forma que aquel valor deja el 50% de las observaciones por debajo de él y el otro 50% por encima de él. Para la ubicación de la posición de la mediana se deben ordenar los datos de forma ascendente.
La mediana es representada por Me. Si el conjunto de datos no se han agrupado, la posición de la mediana se ubica según los siguientes criterios:
Cuando el total de datos (n) es impar, la posición de la mediana estará determinada por la fórmula:

Los datos agrupados son aquellos que se han clasificado en categorías o clases, tomando como criterio su frecuencia. Esto se hace con la finalidad de simplificar el manejo de grandes cantidades de datos y establecer sus tendencias.

Media aritmética

Cuando se agrupan los datos en una tabla de frecuencias, con intervalos, se calcula la media aritmética mediante la siguiente
formula:

Moda

Cuando los datos han sido agrupados en clases o intervalos, la moda se calcula utilizando la ponderación en el intervalo, con el siguiente procedimiento (Posada y Buitrago, 2008):

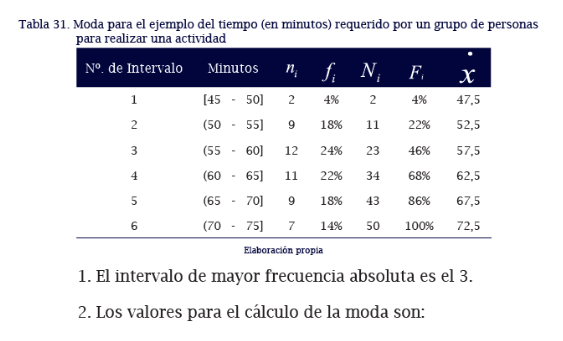
Mediana

Observe el siguiente ejemplo:

https://www.youtube.com/watch?v=G3IXLgozzaghttps://www.youtube.com/watch?v=kek-jrOSuHU