Medidas de dispersión

Medidas de dispersión para datos sin agrupar

Además de las medidas de tendencia central que posibilitan la representación del conjunto de datos por medio de un valor, es necesario conocer la variabilidad o la dispersión que los datos pueden tener en relación a una medida central.
En los análisis estadísticos, las medidas de dispersión que presentan más representatividad son: rango, rango intercuartil, varianza, desviación estándar y coeficiente de variación (Posada y Buitrago, 2008).

https://www.youtube.com/watch?v=Efg6G8vlVUA

Rango

El rango es considerado como la medida de dispersión más simple para el análisis de los datos. No ofrece mucha información sobre la variabilidad de los datos por estar basada sólo en los valores extremos, razón por la cual debe ser usada como complemento de otras medidas de dispersión. Para el cálculo del rango se utiliza la siguiente ecuación:

Rango = valor máximo – valor mínimo

https://www.youtube.com/watch?v=q5bWSTIaV0g

Al calcular la varianza, los datos se elevan al cuadrado, por tanto, las unidades con las cuales se midieron también se elevan al cuadrado, imposibilitando la interpretación. En consecuencia, en la mayoría de los análisis estadísticos se emplea la varianza como una medida que permite comparar la dispersión entre dos o más variables, identificando la de mayor varianza como aquella que posee mayor dispersión o variabilidad. La importancia de la varianza está en que es una medida transitoria para el cálculo de la desviación típica o estándar de un conjunto de datos.

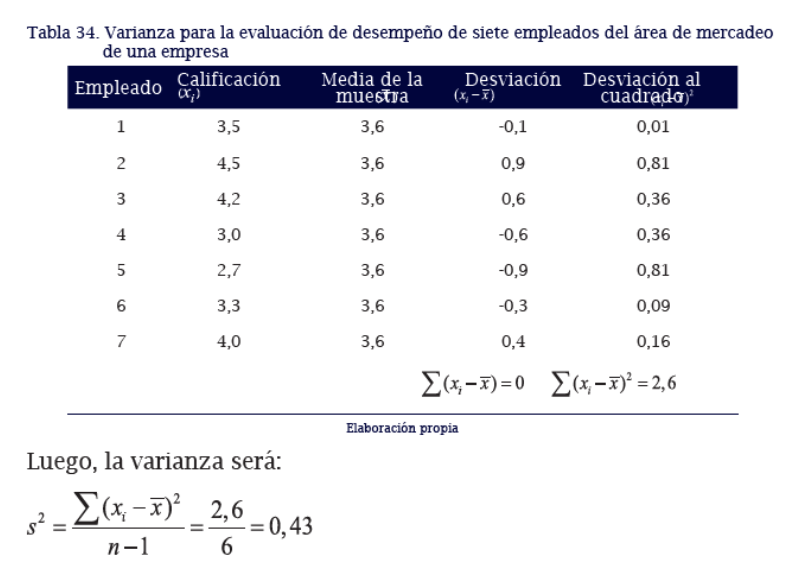
https://www.youtube.com/watch?v=oZRaDwnpXkY&t=304s

Desviación estándar

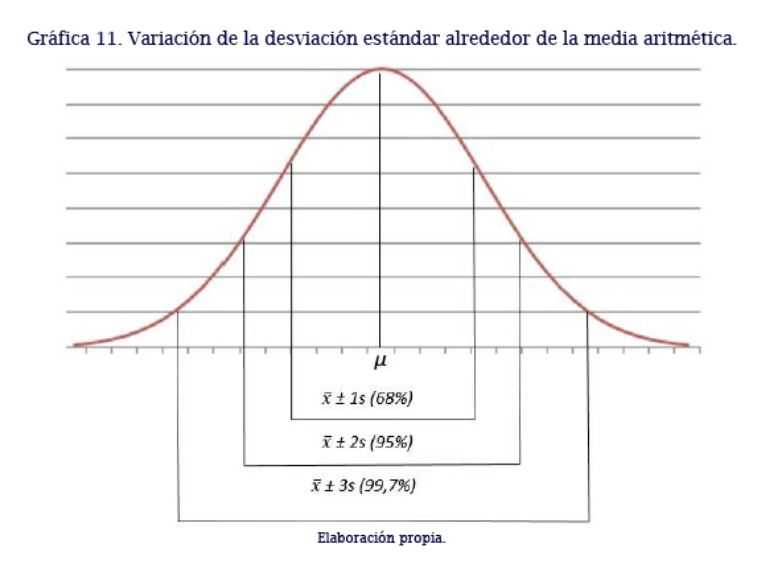
La desviación estándar es considerada la medida de dispersión con mayor representatividad para un conjunto de datos.

https://www.youtube.com/watch?v=hLmsEFNaOgY

Coeficiente de variación

El coeficiente de variación (CV) es una medida que relaciona la desviación estándar con la media aritmética para determinar qué tan homogénea o dispersa es la información. Expresa el porcentaje que representa la desviación con relación a la media aritmética y se calcula por medio de la siguiente ecuación:

El coeficiente de variación, por ser una medida de dispersión relativa, se utiliza para comparar la variabilidad de distintas muestras o poblaciones, aunque tengan unidades de medida diferentes (Triola, 2000).

Medidas de dispersión datos agrupados

Si los datos se agruparon en frecuencias o en intervalos, la varianza puede ser calculada mediante las siguientes formulas:

https://www.youtube.com/watch?v=1myBo87lYyU